8 Major Scale

A scale is a series of pitches generally confined to the span of one octave. All scales are named by identifying the first note of the scale (the root of the scale) and the type of scale. An easy way to think of it is to start on a note and move up the musical alphabet until we get back to our starting note. While there are numerous types of scales, the most commonly used one in Western music, and the one that is the most useful when studying music theory, is the major scale.

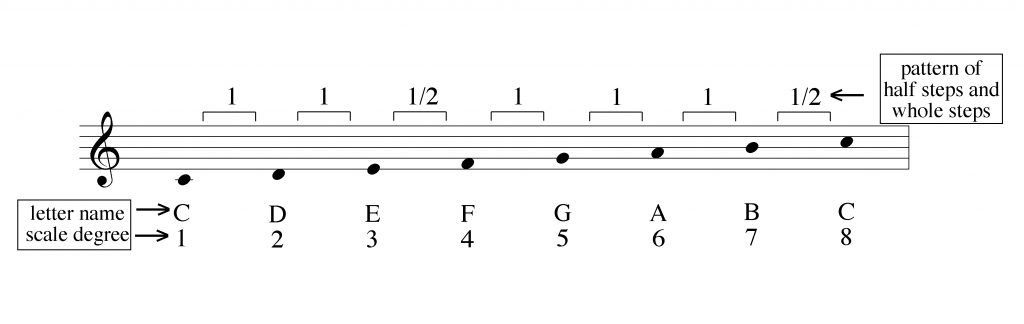
The major scale is a series of semitones and whole tones (two semitones placed together) that form a pattern within an octave. The image below shows the pitches and note names of C major scale, as well as the pattern of whole tones (shown with a 1) and semitones (shown with a 1/2). It also shows the scale degree of each note, meaning its relative position within the scale.

Here is an example of what C major scale sounds like:

When examining the C major scale, we can identify a pattern of whole tone, whole tone, semitone, whole tone, whole tone, whole tone, and semitone between each scale degree and the next. This pattern is true of all major scales, regardless of which note they start on. While C major consists of all the white notes on a piano keyboard, major scales starting on other notes will have a mix of white and black notes.

When looking at the C major scale on a piano keyboard, we can see that every time there is a whole tone in the scale, there is a black note between the two white notes being used in the scale. This is because as the semitone is the smallest distance between two notes; it is also the distance between two keys on the piano, regardless of colour. We can see the semitones found between E and F, as well as B and C. We can clearly see that there isn’t a black note between the white keys, which helps identify the semitones on our major scale.  

To create a major scale starting on G then, we have to re-examine the pattern of tones and semitones and modify to create the correct pattern.

We can see that, while the scale starts correctly, the pattern of tones and semitones deviates from the needed pattern for a major scale after we reach E, or the sixth-scale degree. The distance between the 6 and the 7 should be a whole tone, and currently it is only a semitone. In order to correct this, we need to raise the 7 by one semitone, meaning F to F#, which then not only creates the whole tone needed between the 6 and the 7 but also creates the semitone needed between the 7 and the 8.

If we listen carefully, we can hear that it doesn’t sound correct:

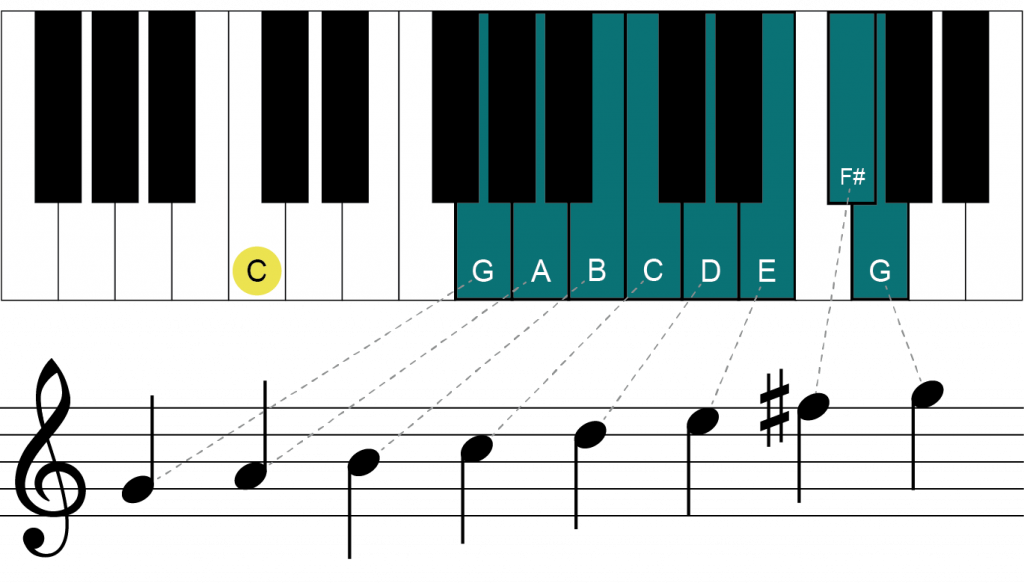
Now that the F has been raised with a sharp, the scale sounds correct.

When starting this process again, but this time starting on F, we can see that the pattern of tones and semitones deviates much earlier in the scale than when starting on G. From A (3) to B (4) is a tone rather than the needed semitone.

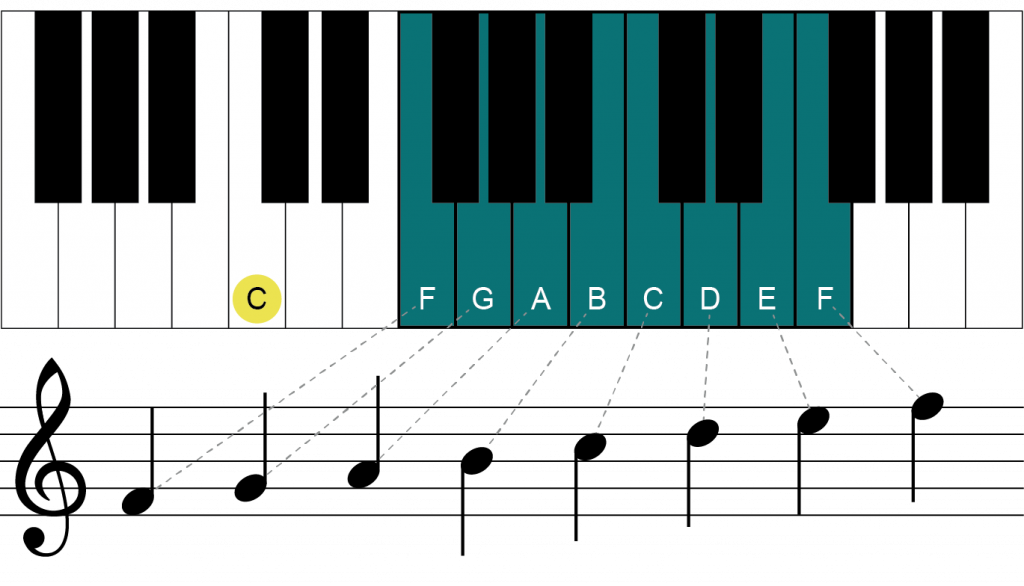
We can hear that the scale currently doesn’t sound like a major scale.

Because the distance between A and B is currently a tone, the B needs to be lowered to a Bb to create the needed semitone. Similar to the G major scale needing the F to be raised, this change not only corrects the error between the A (3) and B (4), but it also creates the proper distance between the B (4) and the C (5).

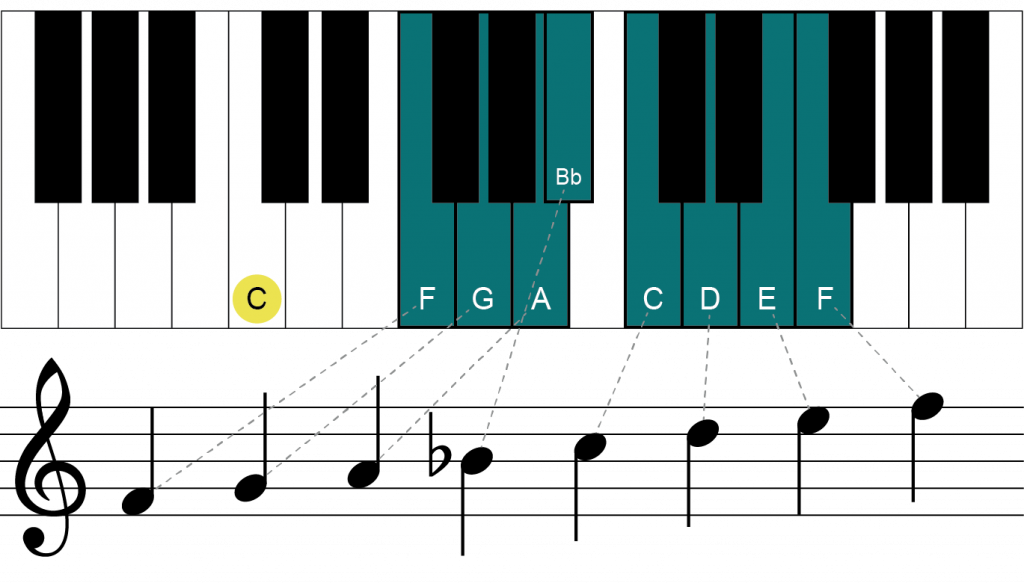
Now that the B has been lowered, the scale sounds correct.

While it is possible to create all the major scales using this pattern of tones and semitones, it is much more beneficial and faster to use and memorize the major key signatures.