In practice, the population standard deviation is usually unknown. It is often estimated by the sample standard deviation

[latex]s = \sqrt{\frac{\sum^n_{i=1}(x_i - \bar{x})^2}{n-1}} = \sqrt{ \frac{\left( \sum x_i ^2 \right) - \frac{(\sum x_i)^2}{n} } {n-1} }.[/latex]

7.2.1 t Distribution and t-Score Table

Recall the distribution of the sample mean [latex]\bar{X}[/latex]: if the population from which we sample is normally distributed or if the sample size is large, it follows that [latex]\bar{X} \sim N(\mu, \frac{\sigma}{\sqrt{n}})[/latex]. For computational simplicity, we often transform [latex]\bar{X}[/latex] into the standardized variable [latex]Z = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}},[/latex] which follows the standard normal distribution. However, when [latex]\sigma[/latex] is unknown, it is estimated with the sample standard deviation [latex]s[/latex], and this leads to a different random variable [latex]t= \frac{\bar{X} - \mu}{s / \sqrt{n}}[/latex], which follows the t distribution with a parameter called degrees of freedom [latex]df = n-1[/latex].

In general, degrees of freedom are the number of independent variables that can take arbitrary values; it equals the number of variables minus the number of relationships among the variables. For example, if two random variables, X and Y, are independent, we have [latex]df =2[/latex]. However, if they satisfy the relationship X+Y=5, then [latex]df = 2-1=1[/latex]. The random variable [latex]t= \frac{\bar{X} - \mu}{s / \sqrt{n}}[/latex] is based on [latex]n[/latex] random variables [latex]X_1,  X_2, \cdots, X_n[/latex] with [latex]\bar X=\frac{X_1+X_2+\cdots+X_n}{n}[/latex]; therefore, we have [latex]n[/latex] independent variables with one relationship. As a result, the degree of freedom is [latex]df=n-1[/latex].

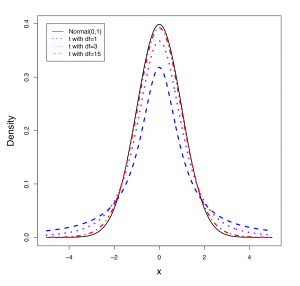
The t density curve is very similar to the standard normal density curve. The following figure shows several t density curves with different degrees of freedom and the standard normal density curve.

Here are the properties of a t distribution:

Unlike the standard normal table (Table II) whose main body gives left-tailed areas under the standard normal density curve, the main body of the t-score table (Table IV) gives t-scores, [latex]t_{\alpha}[/latex], which are defined in a manner analogous to [latex]z_{\alpha}[/latex]. That is, the t-scores [latex]t_{\alpha}[/latex] is the value such that the area to its right is [latex]\alpha[/latex], under the density curve of the t distribution with a given degree of freedom.

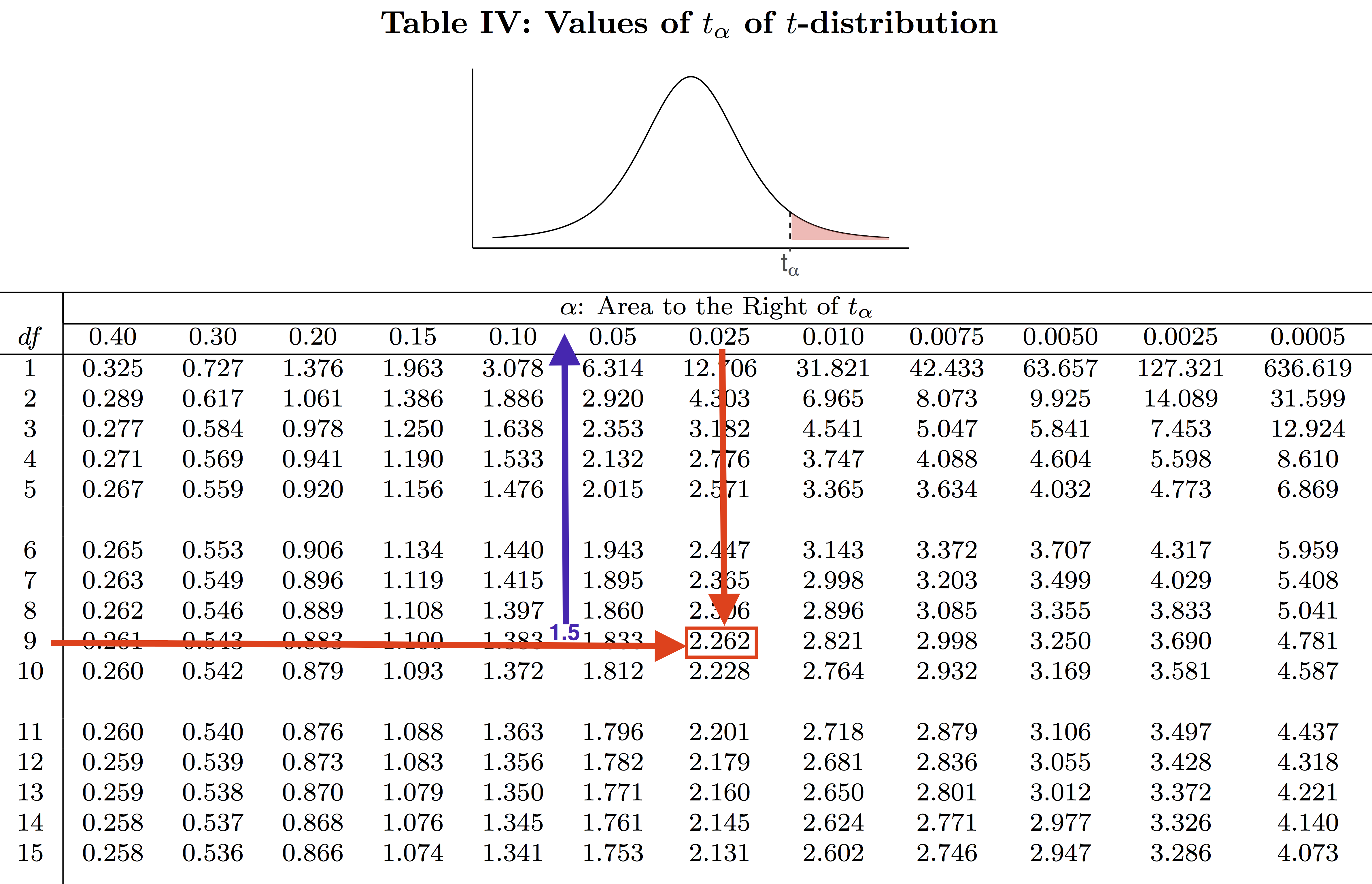
For example, if [latex]n=10[/latex] and [latex]df = n-1 = 9[/latex], then [latex]t_{0.025} = 2.262[/latex]. That is, the t-score 2.262 has an area of 0.025 to its right, under the t-density curve with 9 degrees of freedom. Notice that for each [latex]df[/latex], the t-table lists only 12 t-scores. For this reason, we are often required to approximate the area to the right of a given t-score. For example, to find the area to the right of the t-score 1.5 under the t density curve with [latex]df = 9[/latex], we first locate the t-score 1.5, which is between 1.383 and 1.833; then, if we look at the top of the table, we see that the area to the right of 1.5 is between 0.1 and 0.05. If we use technology, for example, the R commander, we determine that the t-score of 1.5 has a right-tailed area of 0.0839. That is, when [latex]df=9[/latex], [latex]t_{0.0839} = 1.5[/latex].

Exercise: Use of the t-Score Table

Given that [latex]n =15[/latex], use the t-score table (Table IV) to find

1. [latex]t_{0.025}[/latex]
2. [latex]t_{0.005}[/latex]
3. [latex]P(t \geq 2.145)[/latex], which is the area to the right of 2.145 under the t density curve.
4. [latex]P(t \leq -2.145)[/latex], which is the area to the left of -2.145 under the t density curve.
5.  [latex]P(t \geq 2.5)[/latex] , which is the area to the right of 2.5 under the t density curve.

Show/Hide Answer

For [latex]n=15, df= n-1 = 14[/latex]. Hence, we may refer to the bottom row of the table in Figure 7.4 and Figure 7.5.

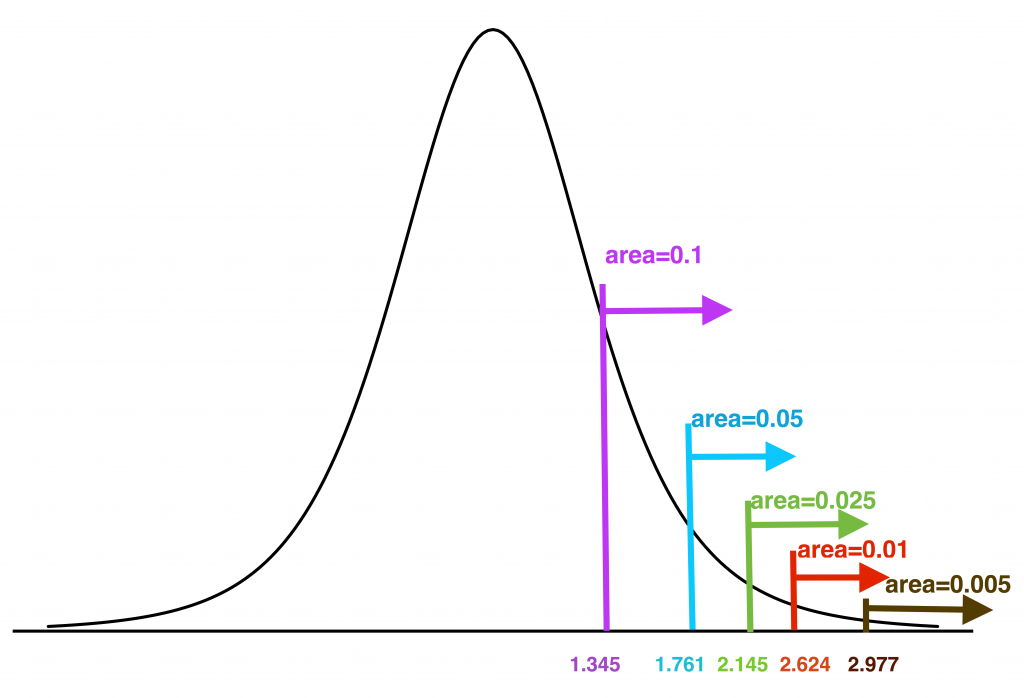
1. [latex]t_{0.025} = 2.145[/latex]
2. [latex]t_{0.005} = 2.977[/latex]
3. Since [latex]t_{0.025}=2.145[/latex], it follows that [latex]P(t \geq 2.145) = 0.025[/latex].
4. First note that the t distribution is symmetric at 0, so the area to the left of -2.145 is the same as the area to the right of 2.145. Therefore, [latex]P(t \leq -2.145) = P(t \geq 2.145) = 0.025[/latex], which is the area under the t density curve to the left of –2.145.
5.  Since 2.145 (which is [latex]t_{0.025}[/latex]) [latex]< 2.5 < 2.624[/latex] (which is [latex]t_{0.01}[/latex]), the area to the right of 2.5 should be somewhere between 0.025 and 0.01. That is, [latex]0.01 < P(t \geq 2.5) < 0.025[/latex].

7.2.2 One-Sample t Interval When σ is Unknown

When the population standard deviation [latex]\sigma[/latex] is unknown and estimated by the sample standard deviation [latex]s[/latex], a [latex](1-\alpha) \times 100\%[/latex] confidence interval is given by a one-sample t interval:

Example: One-Sample t Interval

A computer company claims that the average lifetime of its laptops is about 4 years. A simple random sample of 36 laptops yields an average lifetime of 3.5 years with a sample standard deviation of 4.2 years.

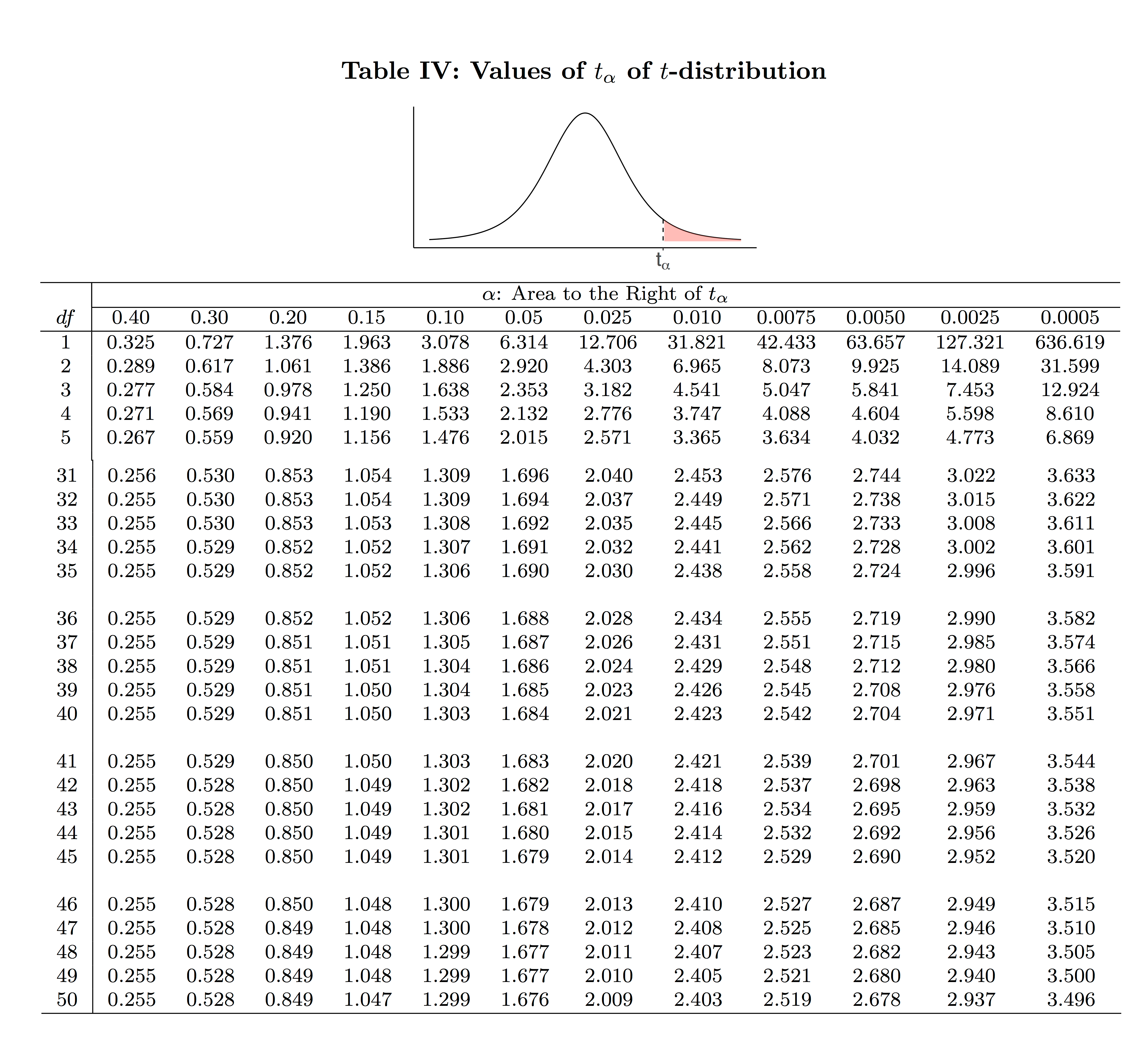
You could use the following truncated Table IV to obtain the t-scores.

1. Obtain a 99% confidence interval for the population mean lifetime [latex]\mu[/latex].
   Check the assumptions:
   1. We have a simple random sample (SRS).
   2. We do not know whether the population is normal or not, but we have a large sample size [latex]n = 36 > 30[/latex].
   3. [latex]\sigma[/latex] is unknown and estimated by [latex]s=4.2[/latex].

   Steps:

   • Find [latex]t_{\alpha / 2}[/latex]: [latex]n = 36, df = n-1 = 36-1 = 35[/latex] [latex]1 - \alpha = 0.99 \Longrightarrow \alpha = 0.01 \Longrightarrow \frac{\alpha}{2} = 0.005 \Longrightarrow t_{\alpha / 2} = t_{0.005} = 2.724[/latex] (using Table IV).
   • Information: [latex]n = 36, \bar{x} = 3.5, s = 4.2[/latex].
   • Interval:  [latex]\begin{align*}\bar{x} \pm t_{\alpha / 2} \frac{s}{\sqrt{n}}&= 3.5 \pm 2.724 \times \frac{4.2}{\sqrt{36}}=(3.5-1.9068, 3.5+1.9068 )\\&=(1.5932, 5.4068).\end{align*}[/latex]

   Interpretation: We are 99% confident that the interval [latex](1.5932, 5.4068)[/latex] contains the population mean lifetime. In other words, we are 99% confident that this computer company produces laptops with a mean lifetime somewhere between 1.5932 and 5.4068 years.

2. Obtain an 80% confidence interval for the population mean lifetime.
   Steps:
   • Find [latex]t_{\alpha / 2}[/latex] : [latex]n = 36, df = n-1 = 36-1 = 35[/latex] [latex]1 - \alpha = 0.8 \Longrightarrow \alpha = 0.2. \Longrightarrow \frac{\alpha}{2} = 0.1 \Longrightarrow t_{\alpha / 2} = t_{0.1} = 1.306[/latex] (using Table IV).
   • Information: [latex]n = 36, \bar{x} = 3.5, s = 4.2[/latex].
   • Interval:
     [latex]\begin{align*}\bar{x} \pm t_{\alpha / 2} \frac{s}{\sqrt{n}}&= 3.5 \pm 1.306 \times \frac{4.2}{\sqrt{36}}= ( 3.5 - 0.9142, 3.5 + 0.9142)\\ &= (2.5858, 4.4142 ).\end{align*}[/latex]

   Interpretation: We are 80% confident that the interval [latex](2.5858, 4.4142)[/latex] contains the population mean life [latex]\mu[/latex]. In other words, we are 80% confident that this computer company produces laptops with a mean lifetime somewhere between 2.5858 and 4.4142 years.

3. Does the confidence interval in part a) provide any evidence against the company’s claim that the average lifetime of this brand of laptops is about 4 years?
   No. Since the interval [latex](1.5932, 5.4068)[/latex] contains 4, we can not reject the claim that the average lifetime is about 4 years.