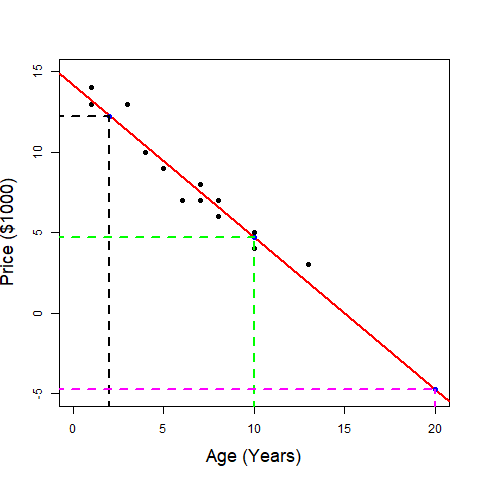
13.3 Prediction and Extrapolation

We can use the least-squares regression line [latex]\hat{y} = b_0 + b_1 x[/latex] to predict the value of the response variable [latex]y[/latex] given the value of the predictor variable [latex]x[/latex]. For example, using the least-squares straight line from the previous exercise, the predicted price of a car that is 2 years old (age=2) is: [latex]\widehat{\mathrm{price}} = 14.118 - 0.9432 \times 2 = 12.2316[/latex] ($1,000, see figure below), or $12,231.6. The predicted price for a 10-year-old car is: [latex]\widehat{\text{price}} = 14.118 - 0.9432 \times 10 = 4.686[/latex] ($1,000, see figure below), which means the price of a 10-year-old car is predicted as $4,686.

When making a prediction, avoid extrapolation, in which [latex]y[/latex]-values are predicted using [latex]x[/latex]-values that are outside of the range of the observed [latex]x[/latex]-values. For example, if we use the least-squares regression line [latex]\widehat{\text{price}} = 14.118 - 0.9432 \times \text{age}[/latex] to predict the price of a 20-year-old car, our estimated price is [latex]\widehat{\text{price}} = 14.118 - 0.9432 \times 20 = -4.746[/latex] ($1,000, see figure below). It does not make sense for an individual to pay $4,746 if he/she wants to sell a 20-year-old car; this is the consequence of extrapolation. This regression line was developed with used cars between 1 and 13 years old; age=20 is outside this range, and we should not use the fitted least-squares line to predict the price of a 20-year-old car. Another example of extrapolation is to predict the height of an adult based on their weight using a regression line (regress height on weight) fitted on the data of children under 10 years old.