4.1 Random Variable
In this section we introduce discrete random variables and their probability distributions.
Given a chance experiment, the collection of possible outcomes is called the sample space, denoted as S. A random variable is a function (or a mapping) from the sample space S into real numbers. Random variables are usually denoted as uppercase letters, such as X, Y, Z. We use the corresponding lowercase letters x, y, z to represent possible values that random variables may attain.
Example: Random Variable
- Consider the chance experiment of flipping a balanced coin twice, the sample space is S = {HH, HT, TT, TH}. Let the random variable X = # of tails. It is a mapping from the sample space S to integers 0, 1, and 2.
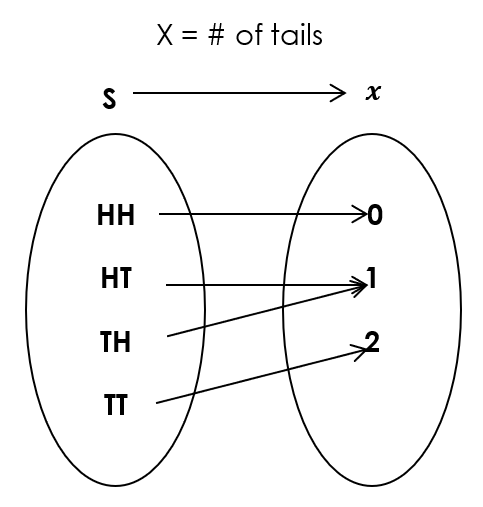
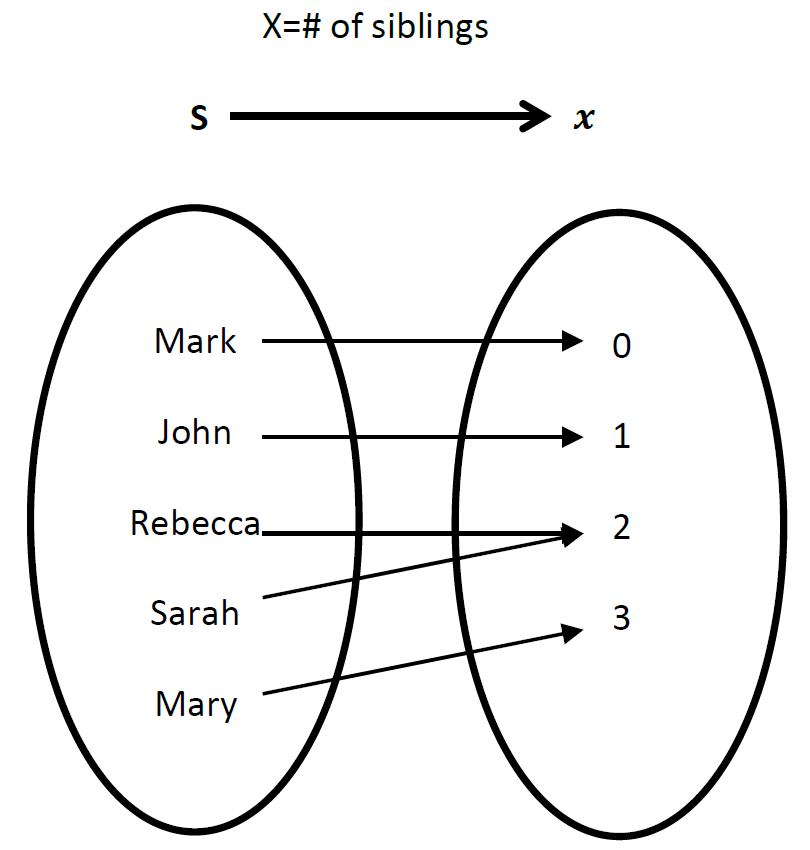
Figure 4.1: Random Variable X=# of Tails. [Image Description (See Appendix D Figure 4.1)] - Five students are asked to report the number of siblings they have; their responses are summarized in the following table:
Name Mark John Rebecca Sarah Mary # of Siblings 0 1 2 2 3 Randomly pick one student and let random variable X = # of siblings the student has. Then X is a mapping from the sample space S = {Mark, John, Rebecca, Sarah, Mary} to the numbers 0, 1, 2 and 3.
In general, a discrete random variable maps the sample space S to numbers that can be listed or counted; a continuous random variable maps the sample space S to an interval that is a subset of the entire real line. If you need to review discrete and continuous data, refer to variables and data in Chapter 1.3.

