10.2 Distribution of the Sample Proportion

Inferences about the population mean [latex]\mu[/latex] are based on the distribution of the sample mean [latex]\bar{X}[/latex]. Similarly, inferences about the population proportion [latex]p[/latex] are based on the distribution of the sample proportion [latex]\hat{p}[/latex].

The population proportion is defined as

[latex]p = \frac{\text{# of individuals having a certain attribute}}{\text{# of individuals in the population}} = \frac{\text{# of successes}}{N}.[/latex]

The population proportion can be regarded as a special type of population mean if we let the variable of interest be an indicator variable as follows:

[latex]x_i = \begin{cases} 1 & \text{if the ith individual has the attribute (a success)}, \\ 0 & \text{if the ith individual does not have the attribute (a failure)}. \end{cases}[/latex]

Then, the population proportion can be rewritten as

[latex]p=\frac{\text{# of individuals having a certain attribute}}{\text{# of individuals in the population}} = \frac{\text{# of successes}}{N} = \frac{\sum x_i}{N}.[/latex]

The variable of interest [latex]X[/latex] has only two possible values: 1 if the individual has the attribute and 0 if not. Randomly select one individual and define [latex]p[/latex] as the probability that this individual has the attribute. As a result, the probability distribution of [latex]X[/latex] is

Table 10.1: Probability Distribution of an Indicator Variable

with a population mean and population standard deviation:

[latex]\mu = \sum x P(X=x) = 1 \times p + 0 \times (1-p) = p,[/latex]

[latex]\sigma = \sqrt{\sum x^2 P(X=x) - \mu^2} = \sqrt{1^2 \times p + 0^2 \times (1-p) - \mu^2} = \sqrt{p - p^2} = \sqrt{p(1-p)}.[/latex]

The sample proportion can be viewed as a special type of sample mean (in the same way that the population proportion can be viewed as a special type of population mean). That is, in a simple random sample of size n, the proportion of individuals with the specific attribute is the sample proportion:

[latex]\begin{align*} \hat{p} &= \frac{\text{# of individuals having a certain attribute in the sample}}{\text{sample size}}\\& = \frac{\text{# of successes in the sample}}{n} = \frac{\sum x_i}{n} = \bar{x} \end{align*}[/latex]

with [latex]x_i = 1[/latex] if the individual has the attribute and [latex]x_i=0[/latex] if not.

Recall from Chapter 6, the sampling distribution of the sample mean [latex]\bar{X}[/latex]:

• Centre: the mean of the sample mean [latex]\bar{X}[/latex] equals the population mean [latex]\mu[/latex]. That is,

  [latex]\mu_{\scriptsize \bar{X}} = \mu.[/latex]

• Spread: the standard deviation of the sample mean equals the population standard deviation divided by the square root of the sample size. That is,

  [latex]\sigma_{\scriptsize \bar{X}} = \frac{\sigma}{\sqrt{n}}.[/latex]

These two arguments are true for any population distribution and sample size n.

• Shape:
  • When the population distribution is normal, [latex]\bar{X}[/latex] is also normal regardless of n.
  • When the population distribution is non-normal but the sample size n is large, [latex]\bar{X}[/latex] is approximately normally distributed. This is guaranteed by the central limit theorem (CLT).

The same conclusions can be applied to the sampling distribution of the sample proportion [latex]\hat{p}[/latex], where the variable of interest is

[latex]X = \begin{cases} 1 & \text{with probability } p \\ 0 & \text{with probability } 1-p \end{cases}[/latex]

with the population mean [latex]\mu = p[/latex] and standard deviation [latex]\sigma = \sqrt{p(1-p)}[/latex]. Therefore, the sampling distribution of the sample proportion [latex]\hat{p}[/latex] is summarized as follows.

Central limit theorem for the sample proportion:

If the sample size n is large enough ([latex]np \geq 5[/latex] and [latex]n(1-p) \geq 5[/latex]), the sampling distribution of the sample proportion [latex]\hat{p}[/latex] is approximately normally distributed.

For example, suppose the population proportion is [latex]p=0.05[/latex]. Then the sampling distribution of the sample proportion [latex]\hat{p}[/latex] is approximately normally distributed if the sample size is at least

[latex]n = \max \left\{ \frac{5}{p}, \frac{5}{1-p} \right\} = \max \left\{ \frac{5}{0.05}, \frac{5}{1-0.05} \right\} = \max \{ 100, 5.26 \} = 100.[/latex]

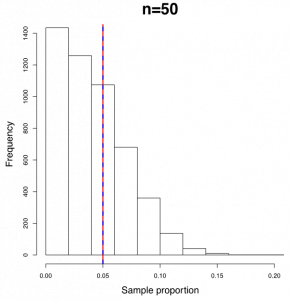
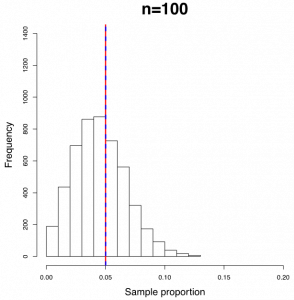
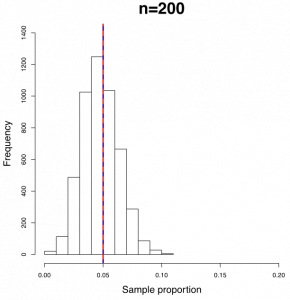
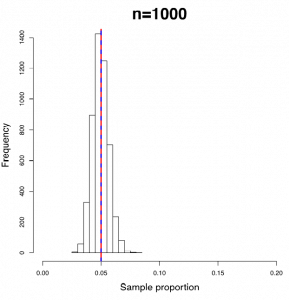
The following figures show the sampling distribution of the sample proportion with [latex]p=0.05[/latex] and sample sizes n = 50, 100, 200, and 1000.

Figure 10.1: Histograms of Sample Proportions with Different Sample Size. [Image Description (See Appendix D Figure 10.1)] Click on the image to enlarge it.

There are several findings:

• The sampling distribution of the sample proportion becomes increasingly normal as the sample size n increases. When n = 50, the sampling distribution of sample proportion is skewed. When n = 100, the distribution is still slightly right skewed. For n = 200 and n = 1000, the sampling distribution appears bell-shaped and symmetric (indicative of a normal distribution).
• The mean of the sample proportion (blue dashed line) is always identical to the population proportion p = 0.05 (red solid line) regardless of the sample size n.
• The standard deviation of the sample proportion decreases as n increases.

To summarize, for [latex]np \geq 5[/latex] and [latex]n(1-p) \geq 5[/latex], [latex]\hat{p} \sim N \left( p , \sqrt{\frac{p(1-p)}{n}} \right)[/latex]. The standardized version of [latex]\hat{p}[/latex] is [latex]Z = \frac{\hat{p} - p}{\sqrt{\frac{p(1-p)}{n}}} \sim N(0,1)[/latex]. As a result, inferences about the population proportions are based on the standard normal distribution.