13.4 Outliers and Influential Observations
In simple linear regression, we must also watch out for outliers and influential observations. Outliers are observations that are far away from the majority of the data. An influential observation is a data point that changes the regression equation dramatically if included. Note that an outlier might or might not be an influential observation.
Example: Outlier and Influential Observations
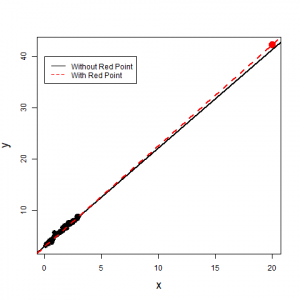
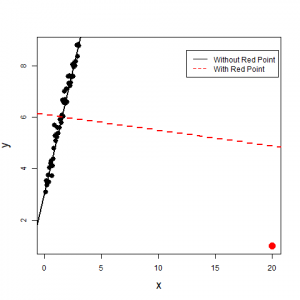
In the following figures, identify whether the red point is an outlier or an influential observation.
 |
 |
The red point on the left panel is an outlier since it is far away from the majority of the data; however, it is not an influential observation since the regression lines are almost identical with and without the red point.
The red point on the right panel is an outlier and an influential observation since including the red point dramatically changes the regression line. Without the red point, the slope of the regression line is positive; the slope becomes negative when the red observation is included. The red observation is also far away from the majority of the data and hence is an outlier.

