5.3 Standard Normal Density Curve

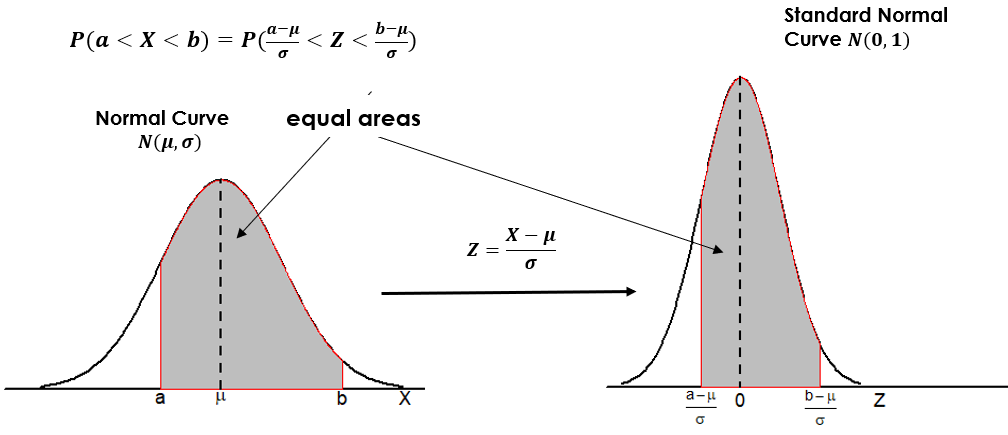
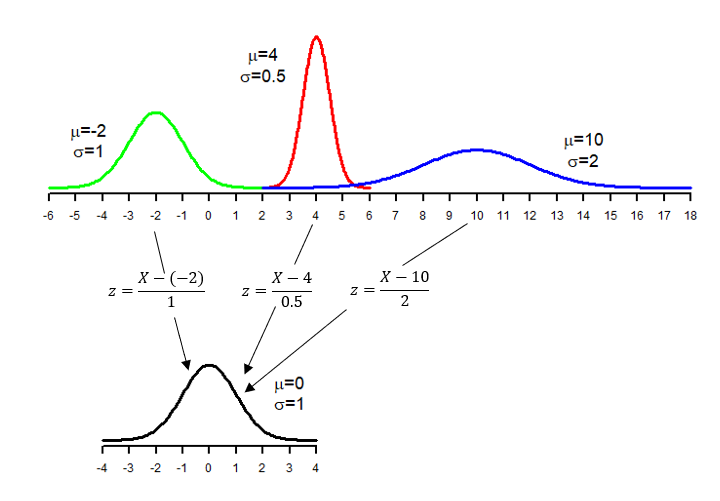
The standardized variable (z-score) has a mean of 0 and a standard deviation of 1. We can also standardize the normal variable [latex]X \sim N(\mu, \sigma)[/latex] by [latex]Z=\frac{X - \mu}{\sigma}[/latex] and [latex]Z[/latex] follows a standard normal distribution with mean 0 and standard deviation 1, i.e., [latex]Z \sim N(0,1)[/latex].

Two normal distributions are shown. The one on the right is the standard z-score. The grey area demonstrates how standardising works. Image description available.
Figure 5.4: Mapping from Normal N(µ, σ) to Standard Normal N(0, 1). [Image Description (See Appendix D Figure 5.4)]

The standard normal density curve has the following properties:

Key Facts: Properties of a Standard Normal Density Curve

  • Total area under the curve is 1.
  • The curve extends from [latex]- \infty[/latex] to [latex]+ \infty[/latex].
  • Symmetric at 0, which means the area to the right of a positive number [latex]a[/latex] is equal to the area to the left of [latex]-a[/latex]. For example, [latex]P(Z \ge 2) = P(Z \le -2).[/latex]
  • Empirical rule:
    1. 68.26% of the observations are within the interval [-1, 1]. The area under the curve between -1 and 1 is 0.6826.
    2. 95.44% of the observations are within the interval [-2, 2]. The area under the curve between -2 and 2 is 0.9544.
    3. 99.74% of the observations are within the interval [-3, 3]. The area under the curve between -3 and 3 is 0.9974.

Standardization converts all normal distributions to a single one—the standard normal distribution. Therefore, we can calculate the probabilities of events relative to any normal distribution using only the standard normal density curve.

Three normal density curves are shown over a horizontal axis. Arrows indicate how each of them can be converted to a standard normal curve. Image description available.
Figure 5.5: Converting Normal Distributions to Standard Normal. [Image Description (See Appendix D Figure 5.5)]

Example: Density Curve and Probability

Suppose the grades in a Statistics class are approximately normally distributed with mean [latex]\mu=70[/latex] and standard deviation [latex]\sigma=10[/latex].

  1. The percentage (proportion, to be more precise) of students with a grade below 60 equals the area under the standard normal curve to the left of -1. The [latex]z[/latex]-score is calculated by [latex]z = \frac{x- \mu}{\sigma} = \frac{60 - 70}{10} = -1[/latex].
  2. The percentage (proportion) of students with a grade above 90 equals the area under the standard normal curve to the right of 2. The [latex]z[/latex]-score is calculated by [latex]z = \frac{x- \mu}{\sigma} = \frac{90 - 70}{10} = 2[/latex].
  3. The percentage (proportion) of students with a grade between 60 and 90 equals the area under the standard normal curve between -1 and 2. Figure 5.4 gives a graphical presentation of this question with [latex]\mu=70, \sigma=10, a=60[/latex] and [latex]b=90[/latex].

 

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics Copyright © 2024 by Wanhua Su is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.