5.4 Using the Standard Normal Table

The standard normal table (usually found in the appendix of a Statistics textbook) can be used to solve problems related to normal distributions.

5.4.1 Find the Area (Probability) for a Given Z-Score

In general, the standard normal table gives the area under the standard normal curve to the left of a specified z-score. Using the table, we can calculate the area under the curve to the left of a z-score, to the right of a z-score, between two z-scores, or beyond two z-scores. Figure 5.6 shows that the area to the left of 1.96 under the standard normal curve is 0.975.

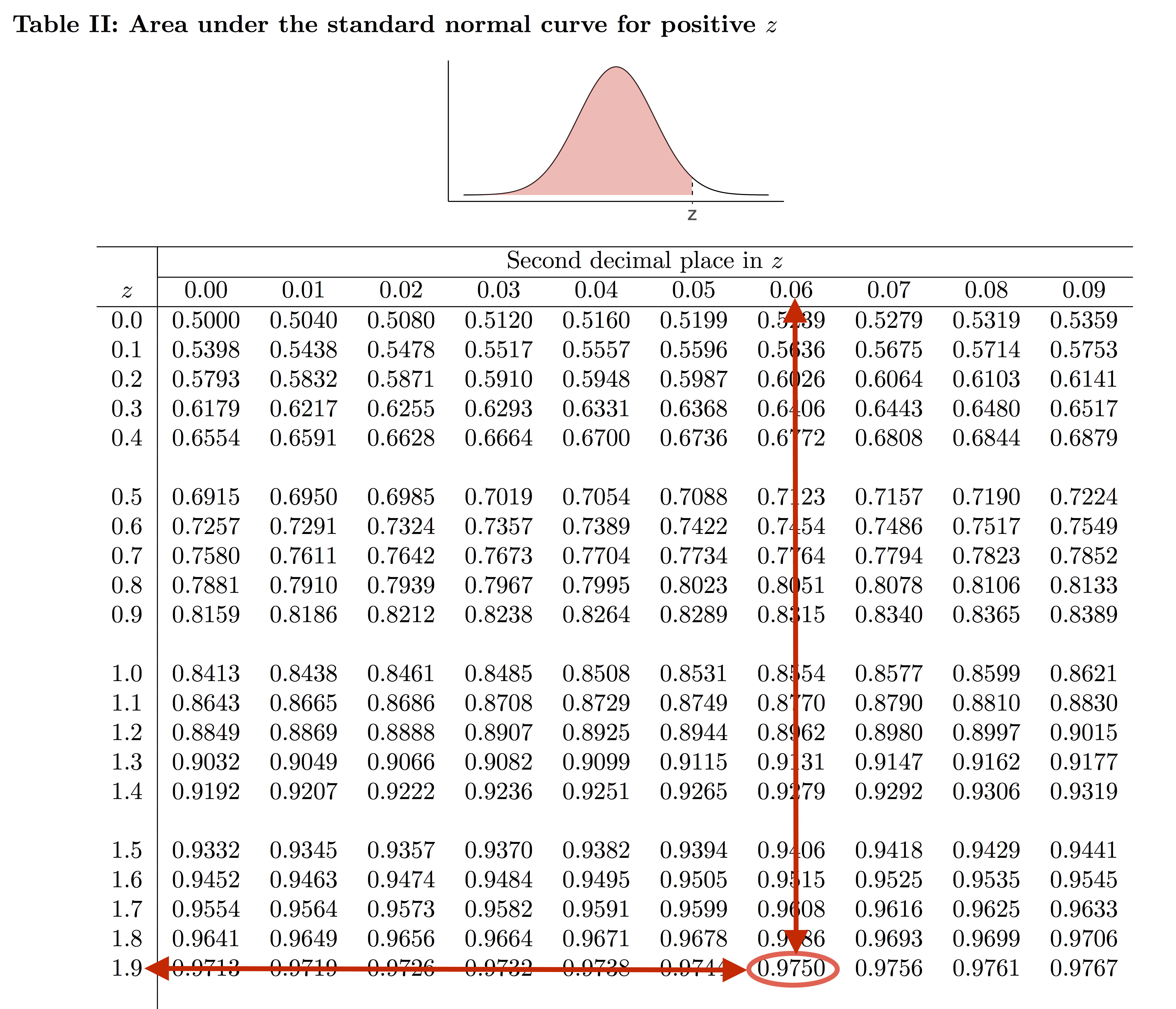
If random variable [latex]Z[/latex] follows a standard normal distribution, more detailed examples of using the standard normal table can be found in Figure 5.7:

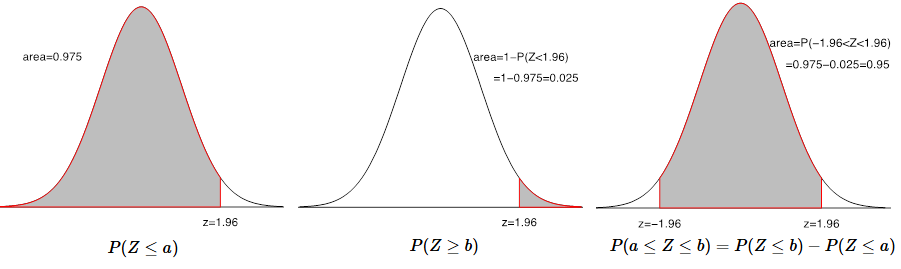
• Left panel: the area to the left of 1.96 is 0.975, i.e., [latex]P(Z<1.96)=0.975.[/latex]
• Middle panel: the area to the right of 1.96 is 0.025. There are two ways to solve this problem:
  1. Recall that the total area under any density curve is one, the area to the right of 1.96 equals one minus the area to the left of 1.96, i.e, [latex]\begin{eqnarray*} P(Z>1.96)&=&\mbox{area under the standard normal curve to the right of 1.96}\\&=&1-\mbox{area under the curve to the left of 1.96}=1-0.975=0.025.\end{eqnarray*}[/latex]
  2. [latex]P(Z>1.96)=P(Z<-1.96)=0.025.[/latex] This is because the standard normal curve is symmetric at 0. The area to the right of 1.96 equals the area to the left of -1.96.
• Right panel: the area between -1.96 and 1.96 is 0.95, i.e., [latex]\begin{eqnarray*}P(-1.96 \lt Z \lt 1.96)&=&\mbox{area between -1.96 and 1.96}\\&=&(\mbox{area to the left of 1.96) - (area to the left of -1.96})\\&=&0.975-0.025=0.95.\end{eqnarray*}[/latex]

[latex]P(Z \leq a)[/latex]	[latex]P(Z \geq b)[/latex]	[latex]P(a \leq Z \leq b) \\ = P(Z \leq b) - P(Z\leq a)[/latex]

Figure 5.7: Area to the Left (left panel), Right (middle panel) of a Z-score, and Between Two Z-scores (right panel). [Image Description (See Appendix D Figure 5.7)]

Example: Finding Areas Under Standard Normal Curve

Suppose that [latex]Z\sim N(0, 1)[/latex], follows a standard normal distribution.

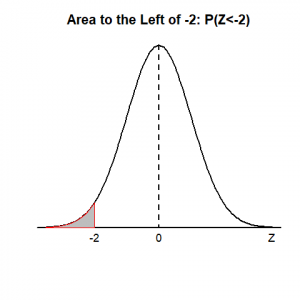
1. Draw a graph to show and find [latex]P(Z<-2)[/latex].

We can find the area to the left of -2 using the standard normal table directly. [latex]P(Z<-2)=P(Z<-2.00)=0.0228.[/latex] Graph showing the area can be found in Panel (1) of Figure 5.6.

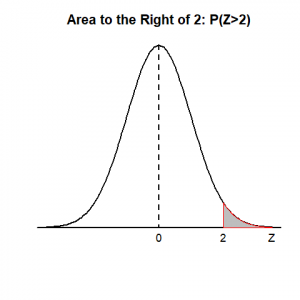
2. Draw a graph to show and find [latex]P(Z>2).[/latex]

This is the area to the right of 2. Recall that the table gives the area to the left of a [latex]z[/latex]-score. There are two ways to answer this question:

• • Apply the symmetry property of the standard normal curve. The standard normal curve is symmetric at 0, and the area to the right of 2 equals the area to the left of -2. [latex]P(Z>2)=P(Z<-2)=0.0228.[/latex]
  • Use the property of a density curve: all density curves have an area of one under the curve. The area to the right of 2 equals one minus the area to the left of 2. [latex]P(Z>2)=1-P(Z<2)=1-P(Z<2.00)=1-0.9772=0.0228.[/latex] Graph showing the area can be found in Panel (2) of Figure 5.8.

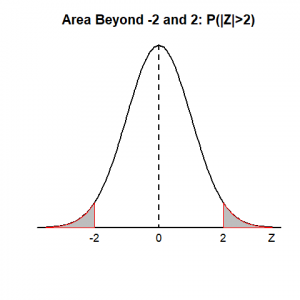
3. Draw a graph to show and find [latex]P(Z<-2 \mbox{ or } Z>2).[/latex]

Area beyond -2 and 2, i.e., to the left of -2 or to the right of 2. The two events {Z<-2} and {Z>2} don’t overlap and, hence, are mutually exclusive; the special addition rule applies. [latex]P(Z<-2 \mbox{ or } Z>2)=P(Z<-2)+P(Z>2)=0.0228+0.0228=0.0456.[/latex] Graph showing the area can be found in Panel (3) of Figure 5.8.

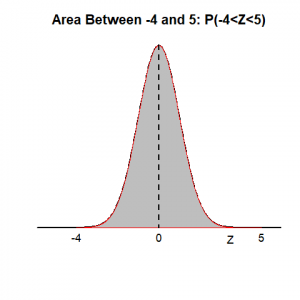
4. Draw a graph to show and find [latex]P(-4 < Z < 5).[/latex]

The area between -4 and 5 equals the area to the left of 5 minus the area to the left of -4. P(-4<Z<5)=P(Z<5)-P(Z<-4)=1-0=1. Graph showing the area can be found in Panel (4) of Figure 5.8.

Note: the standard normal table gives the area (in four decimal places) to the left of the z-score between -3.90 and 3.90. Therefore, the area to the left of any z-score below -3.90 is 0, and the area to the left of any z-score above 3.90 is 1.

(1)

(2)

(3)

(4)

Figure 5.8: Graphs showing the areas under the standard normal curve corresponding to the probabilities in the example. [Image Description (See Appendix D Figure 5.8)] Click on the image to enlarge it.

5.4.2 Find the Z-Score for a Given Area (Probability)

We can use the standard normal table in another way: find the [latex]z[/latex]-score for a specified area or probability (percentage). The steps are as follows:

1. Express the given area in terms of a left-tailed probability (or probabilities if there are 2 z-scores).
2. Search the main body of the standard normal table for the closest value to the left-tailed probability.
3. Obtain the [latex]z[/latex]-score that corresponds to the given area. If multiple values are equally close to the given left-tailed probability, take the average of their corresponding [latex]z[/latex]-scores.

Example: Given the Area, find the corresponding z-score

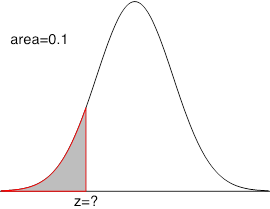
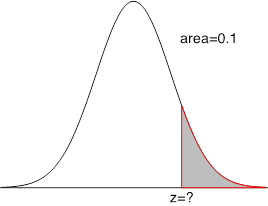
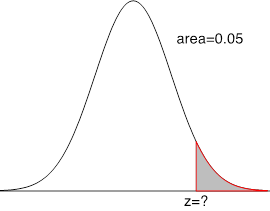
Find the [latex]z[/latex]-score corresponding to the shaded area in each graph:

Closest value to [latex]0.1[/latex] is [latex]0.1003 \Longrightarrow z= -1.28.[/latex]	Method 1: Area on the right is [latex]0.1 \Longrightarrow[/latex] area on the left is [latex]0.9[/latex], the closest value is[latex]0.8997 \Longrightarrow z= 1.28.[/latex] Method 2: due to symmetry, [latex]z=1.28.[/latex]	Area on the right is [latex]0.05 \Longrightarrow[/latex] area on the left is [latex]0.95[/latex], two values [latex]0.9495 (z=1.64)[/latex] and [latex]0.9505 (z=1.65)[/latex] are equally close to 0.95 [latex]\Longrightarrow z = \frac{1.64 + 1.65}{2} = 1.645.[/latex]

[Image Description (See Appendix D Example 5.1)]